 Yes, the thought of two vintage computing devices battling as digital gladiators in a cage match to the death under the watchful eye of our supercomputer overlord, the HAL 9000, is amusing at best. But this is Pi Day, and what better way to celebrate than with silicon blood. Who knows, perhaps this did happen a long time ago in The Grid.
Yes, the thought of two vintage computing devices battling as digital gladiators in a cage match to the death under the watchful eye of our supercomputer overlord, the HAL 9000, is amusing at best. But this is Pi Day, and what better way to celebrate than with silicon blood. Who knows, perhaps this did happen a long time ago in The Grid.
Let the games begin!
Mano-a-mano
In a battle before time itself (I’m referring to the lack of a clock in the Apple II and 41C), this David and Goliath-esque story started to unfold as I was cleaning my office not too long ago. (Cleaning my office is really an excuse to get my retro on.)
I’ve always been a fan (and user) of the Apple II, RPN calculators, and of course, Pi. It’s no wonder that I have stacks of machines, journals, books, magazines, printouts, etc… related to all three topics.
As I was filtering through stacks of papers to determine the value of each scrap of paper, I stumbled across a 1980 article by Ron Knapp, PI TO 1,110 PLACES[1]. I had forgotten about this article. I remember printing it out along with a 1981 followup article by the same author, FASTEST PI TO 1,000 PLACES[2]. At the time I was interested in the relative 1000-digit Pi performance of all ’80s calculators, and gravitated towards the newer, faster code, and had forgotten to read the first article.
So, I read it. Hmmm…
The run-time for this program is relatively short: 30 places in 2 min., 90 places in 9 min., 200 places in 34 min., 1000 places in 11 ½ hr., and 1160 places in 15 ¼ hr. When you consider that an article in “The Best of Micro” some time ago stated that an Apple II had been programmed to calculate “pi” to 1000 places in 40 hours–the run-time for the 41-C, a shirt-pocked calculator, seems very fast indeed[2].
Wow! Really? Can this be true? I was determined to get to the bottom of this. I’ll be “cleaning” my office for a bit longer.
Confirming the Results
 It didn’t take too long to track down the source of Ron Knapp’s statement; Robert J. Bishop’s article, APPLE PI[3]:
It didn’t take too long to track down the source of Ron Knapp’s statement; Robert J. Bishop’s article, APPLE PI[3]:
Since the program is written entirely in BASIC it is understandably slow[3].
Ah ha! BASIC! That explains everything. Right?
I knew from my Apple II days in high school that machine language was faster than BASIC, as was Pascal. But is a circa 1977 computer running BASIC really 4-5 times slower than a circa 1979 pocket calculator? I wanted to see the results myself, and find out why?.
I do not have a clock card in my Apple //c, nor did I have the time to fashion one out of a serial cable and a GPS unit (I’ve done this before), and I am not going to sit around with a stopwatch; I opted to use Virtual ][ on my Mac. IMHO, Virtual ][ is the most authentic Apple II series emulator available. And thankfully Virtual ][ emulates a clock card.
For the HP-41C I’ll be using my HP-41CX. The 41C and 41CX run at the same speed (the X in CX stands for eXpanded memory). Fortunately the CX (unlike the C) has a clock built-in.
I modified both programs to output to a printer and to leverage the clocks so that I could get an accurate reading of the performance. The output with source for the Apple II and HP-41C can be obtained here and here.
The results:
APPLE II
START: MON MAR 7 10:40:40 PM
THE VALUE OF PI TO 1001 DECIMAL PLACES:
3.14159265358979323846264338327950288419
7169399375105820974944592307816406286208
9986280348253421170679821480865132823066
4709384460955058223172535940812848111745
0284102701938521105559644622948954930381
9644288109756659334461284756482337867831
6527120190914564856692346034861045432664
8213393607260249141273724587006606315588
1748815209209628292540917153643678925903
6001133053054882046652138414695194151160
9433057270365759591953092186117381932611
7931051185480744623799627495673518857527
2489122793818301194912983367336244065664
3086021394946395224737190702179860943702
7705392171762931767523846748184676694051
3200056812714526356082778577134275778960
9173637178721468440901224953430146549585
3710507922796892589235420199561121290219
6086403441815981362977477130996051870721
1349999998372978049951059731732816096318
5950244594553469083026425223082533446850
3526193118817101000313783875288658753320
8381420617177669147303598253490428755468
7311595628638823537875937519577818577805
3217122680661300192787661119590921642019
898
END: WED MAR 9 4:27:30 PM
|
41 hours, 46 minutes, and 50 seconds. Confirmed, BASIC is indeed slow.
NOTE: I had to compute 1001 digits of Pi to get 1000 accurate digits.
HP-41C
3.
14159 26535 89793 23846 98336 73362 44065 66430
26433 83279 50288 41971 86021 39494 63952 24737
69399 37510 58209 74944 19070 21798 60943 70277
59230 78164 06286 20899 05392 17176 29317 67523
86280 34825 34211 70679 84674 81846 76694 05132
82148 08651 32823 06647 00056 81271 45263 56082
09384 46095 50582 23172 77857 71342 75778 96091
53594 08128 48111 74502 73637 17872 14684 40901
84102 70193 85211 05559 22495 34301 46549 58537
64462 29489 54930 38196 10507 92279 68925 89235
44288 10975 66593 34461 42019 95611 21290 21960
28475 64823 37867 83165 86403 44181 59813 62977
27120 19091 45648 56692 47713 09960 51870 72113
34603 48610 45432 66482 49999 99837 29780 49951
13393 60726 02491 41273 05973 17328 16096 31859
72458 70066 06315 58817 50244 59455 34690 83026
48815 20920 96282 92540 42522 30825 33446 85035
91715 36436 78925 90360 26193 11881 71010 00313
01133 05305 48820 46652 78387 52886 58753 32083
13841 46951 94151 16094 81420 61717 76691 47303
33057 27036 57595 91953 59825 34904 28755 46873
09218 61173 81932 61179 11595 62863 88235 37875
31051 18548 07446 23799 93751 95778 18577 80532
62749 56735 18857 52724 17122 68066 13001 92787
89122 79381 83011 94912 66111 95909 21642 01989
TIME: 30116.94 SEC
|
8 hours, 21 minutes, and 56.94 seconds.
NOTE: I did not use Ron’s original 1980 program (where the first stone was thrown), but opted to use the optimized 1981 version instead. The Apple II would have taking a a beating in either case.
And the Winner Is…
Ron was right to boast. I have been unable to find any public Apple II results dated before 1982 to take back the title, Microcomputer/Calculator Class: Fastest Pi to 1000 digits.
 To add insult to injury, in 1949, the hulking 30-ton giant ENIAC enslaved a team of four humans and computed Pi to 2037 digits in 70 wall clock hours over a three day holiday weekend. ENIAC throughout the computation also reversed the calculations to check for errors. The humans were leveraged as bio-mechanical RAM since ENIAC could only hold 200 decimal numbers in memory. Team ENIAC worked in shifts collecting, organizing, and feeding IBM punch cards. All compute, check, and human interaction took 70 hours[4, pp. 277-281, 731].
To add insult to injury, in 1949, the hulking 30-ton giant ENIAC enslaved a team of four humans and computed Pi to 2037 digits in 70 wall clock hours over a three day holiday weekend. ENIAC throughout the computation also reversed the calculations to check for errors. The humans were leveraged as bio-mechanical RAM since ENIAC could only hold 200 decimal numbers in memory. Team ENIAC worked in shifts collecting, organizing, and feeding IBM punch cards. All compute, check, and human interaction took 70 hours[4, pp. 277-281, 731].
I’ll demonstrate later that 2037 digits in 70 hours is computationally the same as 1000 digits in ~17 hours. The Apple II in 1978 cannot best a 30-something-year-old cyborg?
Why? Did all three use the same algorithm? In the same way? Are there technological factors or limitations? Can the Apple II best the HP-41C and ENIAC?
To answer all those questions we need to better understand how to compute Pi to 1000 digits.
Computing Pi with arctan
There are many different methods to compute the digits of Pi by hand or with a computer. The arctan formulas since the second half of the 17th century have been the most popular for computing a relatively small (less than a million) number of Pi digits[5, pp. 65, 205]. So it is no surprise that Ron, Robert, and Team ENIAC used arctan as well. Specifically, Machin’s formula.
Machin’s arctan Formula
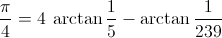
John Machin discovered and used this formula in 1706 to compute the first 100 digits of Pi[5, p. 72]. It has been the most widely used formula by Pi digit hunters until the early ’80’s when the state-of-the-art shifted to Gauss AGM and other exotic formulas[5, pp. 206]. However, Machin is still very popular because it’s easy to implement, fast, and has a low memory footprint. All three are important factors when using retro tech.
Many mathematical functions can be numerically computed with a series which is relatively easy to calculate. The arctan function possesses just such a series which was discovered by James Gregory in 1671[5, p. 67].
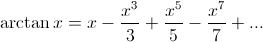
Combine the two and voilà! We have something that we can compute efficiently that will converge quickly.

The first series converges with log10(52) = 1.3979 decimal places per series term and the second converges with log10(2392) = 4.7568 decimal places per series term[5, p. 72].
The total number of terms required for each series for 1000 decimal Pi digits can be calculated with ⎡1000 / log10(52)⎤ = 716 and ⎡1000 / log10(2392)⎤ = 211 respectively. 927 terms total.
NOTE: The ⎡ ⎤ brackets is defined as round up to the next integer.
NOTE: The number of terms does not change if the numeric base for computation changes. IOW, it is constant. More on this later.
TIP: http://www.codecogs.com/latex/eqneditor.php was used to create all equations used in this article.
Arbitrary-Precision Arithmetic
Go ahead, load up that last equation into Apple’s Integer BASIC and see what you get for Pi. 3? Don’t worry, you are are in good company; the biblical value of Pi = 3[6, p. 174] :-). Apple’s Floating Point BASIC doesn’t fair well either; at best, it would have computed 10 or 11 digits.
Clearly we are going to have to create some arbitrary-precision (AP) arithmetic code. The good news is that all we need is add, subtract, multiply, and divide. The simplest method for all four is to go old skool. That’s right, the same way you learned how to do this in elementary school is still applicable today. Simply represent each digit in an array and perform the operations the same way you would with pen and paper. Get out a pen and paper and try it!
It’s easier than it sounds. Although the adds and subtracts will be AP +/- AP, the multiply and divides will be AP ∗/÷ SP (single-precision). Now that’s even easier. AP:AP mult/div is harder and the subject of many papers and AP libraries.
For each operation, as your code loops from the least significant digit to the most significant digit (except divide, go the other way), the four arithmetic routines will perform two basic operations per iteration; add, sub, mult, div, and then a carry. I understand that this is an oversimplification, and if you want a clearer understanding, then I suggest you look at some code. However, the point I am trying to make is that if the number of digits doubles (e.g. computing Pi to 2000 digits), then the number of operations for AP:AP add/sub and SP:AP div/mult also doubles. It also works the other way. If I can half the number of digits, then I half my number of operations, and therefore half the time for basic arithmetic operations.
Covering Your Bases
The amount of effort it takes an 8-bit computer to add two base 10 numbers is the same effort as adding two base 256 (28) numbers. Therefore, if you can pack your 1000 digit base 10 arrays into fewer base 256 digits, then you can also reduce the number of operations and get a proportional speed up in time. Your new array size will = ⎡number of decimal digits / log10base⎤.
A few examples based on 1000 decimal digits of Pi:
| Base |
Calculation |
Array Size
|
| 10 |
⎡1000 / log1010⎤ |
1000
|
| 28 (256) |
⎡1000 / log10(28)⎤ |
416
|
| 216 (65536) |
⎡1000 / log10(216)⎤ |
208
|
| 100,000 |
⎡1000 / log10100,000⎤ |
200
|
| 10,000,000,000 |
⎡1000 / log1010,000,000,000⎤ |
100
|
The speed-up should be proportional to the array size assuming that a larger base will not have a disproportional overhead. E.g. The 6502, an 8-bit processor, will take more that twice the instructions to add two 16-bit numbers compared to two 8-bit numbers. However using 16-bit numbers on an 8-bit system is still more efficient that using base 10.
There is a caveat when not using base 10, 100, 1000, etc…; the end result must be converted back to base 10 if you are truly computing 1000 decimal digits of Pi. This adds a bit of overhead to the end of the computation, however it is only a fraction (e.g. 1/6th for base 216 to base 10) of the total computation.
I am assuming that ENIAC can leverage it’s double precision support and use base 1010 (10,000,000,000) and therefore only require an array of 100 base 1010 digits for 1000 decimal digits of Pi. Ron’s HP-41C program uses base 105 (100,000) requiring only 200 base 105 digit arrays. Robert’s Apple Pi uses base 10 requiring 1000 digit arrays.
This begins to shed some light on why Apple Pi performs so poorly. If Apple Pi could use base 100,000 or base 10,000,000,000 then its time would be reduced by a factor of 5 and 10 respectively. However, Integer BASIC and the 6502 are not designed to support this. ENIAC and the HP-41C are both designed and optimized for base 1010. As they should be; they are calculators.
Computation Complexity
Earlier I said, I’ll demonstrate later that 2037 digits in 70 hours is computationally the same as 1000 digits in ~17 hours.
That statement makes two assumptions. The first is that Team ENIAC used the Gregory expansion of Machin’s arctan formula, and the second is that their AP arithmetic scaled linearly. If that is the case, as is the case with Ron’s and Robert’s programs, and since the number of terms and the number of digits is a fixed ratio based on the desired number of digits; then if the number of desired digits double, then so does the number of terms to be computed and the size of the array to hold the digits, and therefore the amount of computation is double * double. IOW, the computational complexity is O(n2).
Simply put, if I double the digits the time increases by four. Therefore, the estimated time for ENIAC to compute 1000 digits is: 70 hr * (1000/2037)2 = 16.87 hr.
Back to Apple Pi
The number of terms to be computed will be constant regardless of the program’s numeric base. That leaves optimizing the arithmetic routines. Assuming that Robert’s BASIC program could be rewritten in base 256 (and it cannot without a lot of effort; effort that would not yield sufficient benefit), then the best speed up would be 41.78 hr * (416/1000) = 17.38 hr. Still deficient.
When writing fundamental AP routines it helps to have unsigned double precision integer support; if not, make your base the square-root of (the largest positive integer + 1), e.g. the largest HP-41C positive integer is 9,999,999,999, making the optimal base 100,000 since the HP-41C does not have double precision integer support. Because of the wacky integer support in Integer BASIC, the largest base would be 181 and not offer up enough performance.
Bottom line, Integer BASIC is most likely our culprit. In 1978 Robert had very few options. BASIC and assembly language were the dominate languages, and if I were in Robert’s shoes I would have picked BASIC too (Robert wrote the program in less than 40 hours)[3]. However, there was another option; Apple FORTH from Programma Consultants[7, p. 26]. And by 1980, when Ron first mentioned the Apple II’s poor performance, there were many more Apple languages to choose from, such as FORTRAN and Pascal.
Pi Day Rematch: Apple II vs. HP-41C
FORTH seems promising for a few reasons; one, it was available in 1978; two, it’s most like RPN, making a comparison to the 41C a bit more apples to apples; and three, with FORTH it will be easy to use a larger base (I used base 216) thus reducing the size of the arrays. Lastly, FORTH is fast.
Unfortunately I was unable to locate a copy of Apple FORTH from Programma Consultants, so I opted to use Mad Apple Forth (MAF) as a substitute. My program with timings can be located here. I didn’t have time to figure out how to access the clock card from MAF, so I used the Virtual ][ record function and then noted the time stamps on the output.
Start: 22:44:47
Print: 23:05:24
End: 23:09:43
Total Time: 00:24:56
The HP-41C and ENIAC were both schooled by the Apple II with FORTH.
HP-41C cries foul!
If you could only use what came in the box with your Apple II or HP-41C, then what would be the results? Fortunately the Apple II mini-assembler is in the box.
In 1982 Glen Bredon wrote an APPLE PI program in assembly that blows the battery door off the 41C with a time of 194 seconds. Game over! The Apple II wins again!
My 1496 sec. FORTH version doesn’t hold an LED to assembly.
If you are looking for Glen’s program, it is packaged with the Merlin Assembler.
HP-41C Machine Language
To be thorough I asked a friend of mine to compute Pi on the 41C with a 100% machine language (ML) program. He came back with 5 hours, 9 minutes. No question, the Apple II is king.
Victory Lap
In my quest to best the 41C, I tried C as well. The C language hit the seen in the mid ’80s making it easier to write and port over existing Pi programs.
Why not rub it in a bit?
| C Version |
C Year |
Base |
Time (s)
|
| Aztec K&R C 3.2b |
1986 |
216 |
2180
|
| Aztec K&R C 3.2b |
1986 |
10 |
6746
|
| cc65 ANSI C 2.12 |
2010 |
216 |
1764
|
| cc65 ANSI C 2.13 |
2010 |
216 |
1514
|
| cc65 ANSI C 2.13 |
2010 |
10 |
4241
|
Summary
BASIC sucks. The HP-41C is truly awesome, and for a time bested the Apple II in the Fastest to Compute 1000 digits of Pi benchmark. But, in the end, the true potential of the Apple II smoked the 41C.
BTW, you’ll never need more than 50 digits of Pi[5, p. 153].
On the other hand…
To continue reading this fascinating tale click here.
Some Great Pi Books
If you like Pi, especially computing Pi, then I recommend the following three books[4, 5, 6]:

Print References
- Knapp, Ron. PI TO 1,110 PLACES. PPC Calculator Journal Jun. 1980: 9-10.
- Knapp, Ron. FASTEST PI TO 1,000 PLACES. PPC Calculator Journal Aug.-Dec. 1981: 68-69
- Bishop, Robert J. APPLE PI. MICRO THE 6502 JOURNAL Aug.-Sep. 1978: 15-16.
- Berggren, Lennart, Jonathan M. Borwein, and Peter B. Borwein. Pi, a source book . 3rd ed. New York: Springer, 2004. Print.
- Arndt, Jörg, and Christoph Haenel. [Pi] – unleased . 2. ed. Berlin: Springer, 2001. Print.
- Beckmann, Petr. A history of [pi] (pi) . 4th ed. New York: Barnes & Noble, 19931971. Print.
- Apple Computer Inc. the best of the user group newsletters for 1978. Contact ’78 Dec. 1978: 26.
Credits
- Pi Day Deathmatch Poster. Dhemerae Ford (dhemerae@gmail.com).
- ENIAC photo (linked). Wikipedia.
 Well, Pi Day has come and gone, so what’s left for a Pi nerd to look forward to? Tau Day? Heresy! That other Pi Day, July 22nd (22/7)? Pa-lease. Accept the fact that it’s OK to talk about Pi when it’s not Pi Day? Sure, why not?
Well, Pi Day has come and gone, so what’s left for a Pi nerd to look forward to? Tau Day? Heresy! That other Pi Day, July 22nd (22/7)? Pa-lease. Accept the fact that it’s OK to talk about Pi when it’s not Pi Day? Sure, why not? No, I didn’t compute Pi on my way to Paris, but just knowing that I could have with my 41CX in my pocket reassured me. :-)
No, I didn’t compute Pi on my way to Paris, but just knowing that I could have with my 41CX in my pocket reassured me. :-) William Shanks (1812 – 1882) was an amateur mathematician and IMHO is still the king of all Pi nerds. William Shanks computed Pi to 707 places over a 15+ year period with nothing but pen, paper, and his wits[2, pp. 305]. A stunning achievement and the last computation of its kind, however, there is an error, can you see it?
William Shanks (1812 – 1882) was an amateur mathematician and IMHO is still the king of all Pi nerds. William Shanks computed Pi to 707 places over a 15+ year period with nothing but pen, paper, and his wits[2, pp. 305]. A stunning achievement and the last computation of its kind, however, there is an error, can you see it?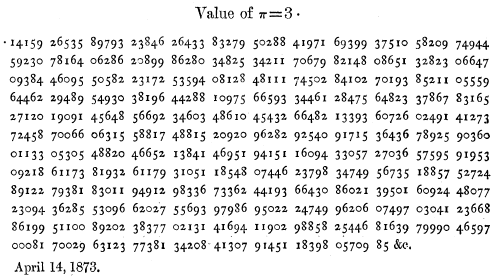




 Yes, the thought of two vintage computing devices battling as digital gladiators in a cage match to the death under the watchful eye of our supercomputer overlord, the HAL 9000, is amusing at best. But this is Pi Day, and what better way to celebrate than with silicon blood. Who knows, perhaps this did happen a long time ago in
Yes, the thought of two vintage computing devices battling as digital gladiators in a cage match to the death under the watchful eye of our supercomputer overlord, the HAL 9000, is amusing at best. But this is Pi Day, and what better way to celebrate than with silicon blood. Who knows, perhaps this did happen a long time ago in  It didn’t take too long to track down the source of Ron Knapp’s statement; Robert J. Bishop’s article, APPLE PI[3]:
It didn’t take too long to track down the source of Ron Knapp’s statement; Robert J. Bishop’s article, APPLE PI[3]: To add insult to injury, in 1949, the hulking 30-ton giant
To add insult to injury, in 1949, the hulking 30-ton giant 